Data Link Layer

• Responsible for taking the data and transforming it into a frame with header control and address information
• Physical path communication
• Error detection
• Error correction
• Resolve competing requests

Noise and Errors

Noise is always there. If there’s too much noise in a communication line, signal will be lost or corrupted.

White noise

• Also known as thermal or Gaussian noise
• Relatively constant and can be reduced
• Strong white noise can completely disrupt the signal

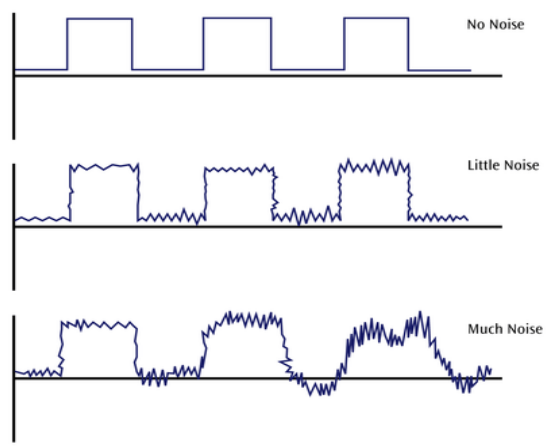
Impulse Noise

• One of the most disruptive forms of noise
• Random spikes of power
• Difficult to remove from an analog signal
• Can damage more bits if the bit rate is higher

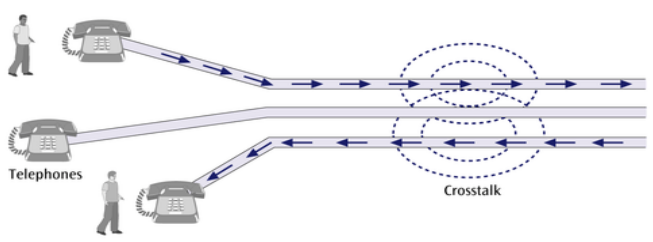
Crosstalk

• Unwanted coupling between two different signal paths
• Relatively constant and can be reduced with proper measures

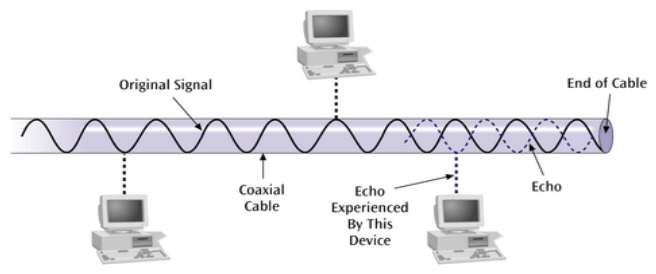
Echo

• Reflective feedback of a transmitted signal as the signal moves through a medium
• More often occurs in coaxial cable
• If the echo is bad enough it could interfere with original signal
• Relatively constant and can be significantly reduced

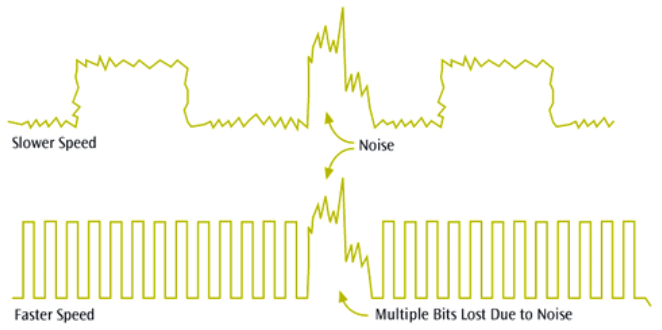
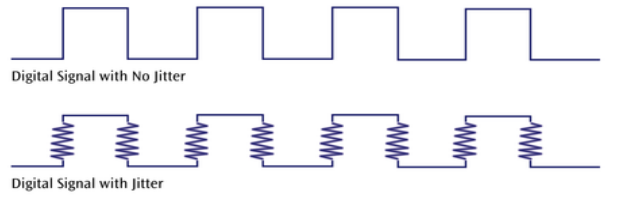
Jitter

• Caused by small timing irregularities during the transmission of digital signals
• Occurs when a digital signal is repeated over and over
• Jitter causes systems to slow down their transmission
• We can reduce jitter through shielding

Delay distrortion

• Occurs because of the velocity of a propergating signal over a medium varies with the frequency of the signal
• Can be reduced using equalizers

Attenuation

• The continuous loss of a signal’s strength as it travels through a medium
• To mitigate
  • Use less lossy medium
  • Use amplifiers

Distortion

• As signals travel it get distorted
  • Change shape
  • Successive bits may merge

Interference

• Unwanted signal from outside sources
  • Difficult to diagnose

Error Prevention

• Proper shielding of cables
• Replacing older media with new equipment
• Proper use of repeaters and amplifiers
• Observing stated capacities of the media

Information Redundancy

Coding

• A data word with d bits is encoded into a code-word with c bits c > d
• To extract original data - c bits must be decoded
• If the c bits do not constitute a valid code-word, an error is detected
• For certain encoding schemes - some types of errors can also be corrected

Separability of a Code

• A separable code has separate fields for the data and code bits
• When decoding we can disregard code bits
• Code bits can be processed separately to verify the correctness of the data
• A non-separable code has the data and code bits integrated together

Parity Codes

• Simplest of the codes
• Parity code includes d data bits and an extra bit to hold the parity
• Even parity :
  • Total number of 1’s of the d+1 length word (including parity bit) is even
• Odd parity:
  • Total number of 1’s of the d+1 length word (including parity bit) is odd

2 Dimensional Parity

• Uses both Longitudinal Redundancy Check (LRC) and Vertical Redundancy Check (VRC)
• Identifies a unique erroneous bit

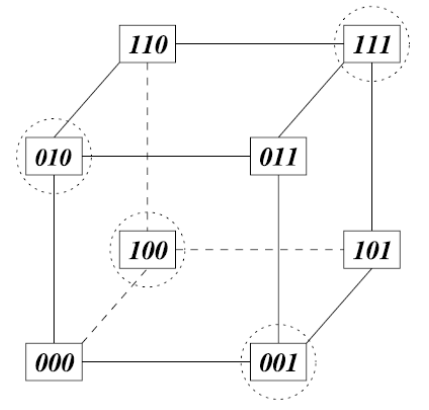
Hamming Distance

• Hamming distance between two code-words shows the number of positions in which the two words differ
• Two words are connected by an edge if their hamming distenace is 1

Hamming Code

• Based on Hamming distance
• Assigns multiple parity bits to cover each bit of data
• Many different hamming code schemes exist
  • Ex: (7,4) Single Error Correcting Hamming Code

(7,4) Single Error Correcting (SEC) Hamming Code

• Can correct 1-bit errors
• Calculating parity bits
  • where r = number of parity btis, m = message bits
• Ex: f m=4, r = 3

Parity Bits placement

• In the resulting codeword, parity bits can be placed at different places. Placement affects how easy/difficult to detect and correct errors
• One way is to place parity bits at paces corresponding to powers of 2

Parity bit coverage

(7,4) Hamming code uses 3 parity bits (,,) , 4 data bits for a 7 bit codeword Each parity bit covers specific bit positions

• P₁ (position 1): Covers positions 1, 3, 5, 7 → P₁
  • Covers positions with bit 0 = 1₂
  • P₁ = XOR of bits at positions 1,3,5,7
• P₂ (position 2): Covers positions 2, 3, 6, 7 → P₂
  • Covers positions with bit 1 = 1₂
  • XOR of bits at positions 2,3,6,7
• P₄ (position 4): Covers positions 4, 5, 6, 7 → P₄
  • Covers positions with bit 2 = 1₂
  • XOR of bits at positions 4,5,6,7 For example let’s take a message m = 1001

Error Detection

When receiving the code-word use parity bits to check the parity of each parity bit

• P₁ check: positions 1,3,5,7 → result 0101 = 0 (even parity ✓)
• P₂ check: positions 2,3,6,7 → result 0111 = 1 (odd parity ✗)
• P₄ check: positions 4,5,6,7 → result 1011 = 1 (odd parity ✗) The syndrome is formed by combining the parity bits ex: 110₂ = 6₁₀ (6th bit is the wrong bit) This syndrome value shows the place of the error bit

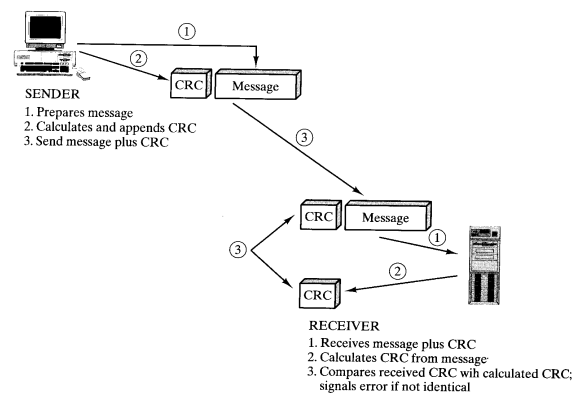
Cyclic Redundancy Checksum (CRC)

• A non separable code
• Treats the packet of data to be transmitted as a large polynomial.
• Takes the message polynomial and using polynomial arithmetic, divide it by a given generating polynomial
• Quotient is discarded, but the remainder is attached to the end of the message (remainder (mod) arithmetic)
• Message (with the remainder) is transmitted to the reciever
• The reciever divides the message and remaider by the same generating polynomial
• If remainder not equal to zero, there was an error during transmission

CRC Example

• Message = 101101
• CRC Polynomial = x³ + x² + 1 = 1101 (in binary)
• Number of CRC bits = 3

Step 1: Append zeroes to your message

Add 3 zeros (number of CRC bits) to the end of your message

• Original message: 101101
• Message with zeros: 101101000

Step 2: Perform modulo-2 long division

Divide the extended message (101101000) by the polynomial (1101) using XOR operations instead of regular subtraction:

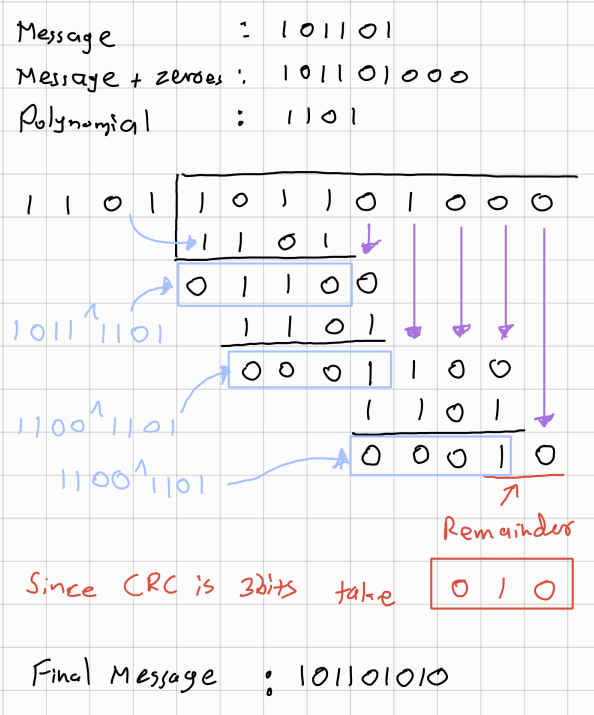
Therefore complete code-word : 101101010